New paper on reconciling taxonomy and phylogeny
27 Sep 2011, by Erick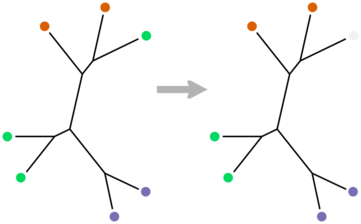 As some of you know, we are currently improving methods to perform taxonomic classification using phylogenetic placements.
In doing so, we noticed something not-so-surprising right away: when the taxonomy and the phylogeny disagree, it makes taxonomic classification difficult.
I starting looking around for tools to evaluate discordance between a taxonomy and a phylogeny, but I didn’t find anything.
As some of you know, we are currently improving methods to perform taxonomic classification using phylogenetic placements.
In doing so, we noticed something not-so-surprising right away: when the taxonomy and the phylogeny disagree, it makes taxonomic classification difficult.
I starting looking around for tools to evaluate discordance between a taxonomy and a phylogeny, but I didn’t find anything.
There is an appropriate formulation in the CS literature, in terms of trees with colored leaves. The minimal convex uncoloring of such a tree is the smallest set of leaves whose colors have to removed such that each remaining color appears in exactly one non-overlapping region of the tree. We can formalize the concordance between a taxonomy and a phylogeny at a given rank by taking the coloring that is induced by the taxonomic classifications at that rank and finding the corresponding minimal uncoloring. The leaves that have to get uncolored are the minimal such set that don’t “fit” according to the phylogeny.
Moran and Snir made this definition and did the foundational work in this area, showing that the problem is NP-hard and fixed parameter tractable. For leaf colorings they have a very elegant dynamic program that uses the Hungarian algorithm to solve the problem. It’s exponential in the total number of colors violating convexity, and works best for trees of large degree.
For our application to taxonomy, the colors aren’t spread uniformly over the tree, but rather are localized (for the most part, they aren’t that far off).
Thus it makes sense to develop an algorithm that is exponential in a measure of local nonconvexity, rather than in the total number of nonconvex colors.
Also, we usually deal with binary trees.
Aaron G and I developed an algorithm that’s specialized to this setting, and it includes a branch-and-bound that can save orders of magnitude of computation time and space.
It’s available as rppr convexify in the dev branch of the pplacer suite.
This was a fun project, and I’m happy that we have a practically useful tool for this problem. It’s Aaron’s first paper, which makes me proud, and I definitely needed his coding skills for the rather involved dynamic program. If you are interested, the paper is up on the arXiv.