How well do MCMC methods work on the discrete space of phylogenetic trees?
13 May 2014, by Erick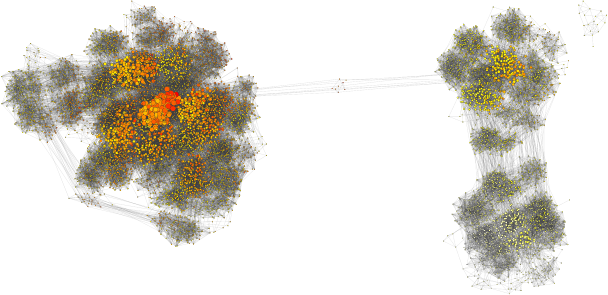
The Bayesian approach to phylogenetics enables, in principle, sampling from the posterior distribution on phylogenetic trees and parameters given some data and a prior. Some wonderful research in phylogenetics been done using this Bayesian perspective, and it allows to estimate the quantities we care about in a rigorous framework. In order to get posteriors on trees and parameters, it is common to use Markov chain Monte Carlo (MCMC), which is a method for setting up a simulation such that the amount of time spent in a given state is proportional to its posterior probability (if you haven’t read the original article suggesting the method I recommend taking a look).
However, we can only be sure that we are getting a good posterior probability estimate if we run the MCMC algorithm for an infinite time. We don’t have that much time, which raises the question of how quickly MCMC converges to this stationary posterior probability distribution. Mossel and Vigoda cooked up a particularly nasty data set which they proved took a very long time to converge (although Ronquist and co-authors were not convinced because the data set was unrealistic, and because M & V didn’t consider an extension to MCMC found in MrBayes). There have been a number of interesting papers looking at convergence time on empirical data sets, including Lakner et al and Höhna and Drummond.
It’s straightforward to consider convergence of real parameters (such as mutation rates), but thinking about trees (by which here we mean tree topologies) is trickier. One can’t consider simple metrics such as total variation distance on the empirical distribution because there are too many trees. What’s needed is a way to give structure to the collection of trees such that we can visualise these posterior distributions. For example, Hillis, Heath, and St. John used the Robinson-Foulds distance to visualize tree space using multidimensional scaling. One might build on this approach by considering other distances and other means of using the distances.
Chris Whidden, in his thesis work, published a string of remarkable papers with his PhD advisors Rob Beiko and Norbert Zeh making it possible to compute a distance between trees called the Subtree-Prune-Regraft distance (SPR) for moderately-sized trees. This distance is especially useful for analyzing MCMC chains because phylogenetic MCMC algorithms use SPR or SPR-like rearrangements to move around tree space.
When he joined the group, we thought it would be fun to use SPR distances to understand convergence of MCMC on real data sets, and to take a primarily graph-based, rather than projection-based approach. We have done so and the results are published in Systematic Biology. Using this approach, we can see multiple peaks as being clusters of points that are not so well connected between one another (see above image). We also find cases where the clade-based approximation to tree posterior probability (see Höhna and Drummond and Larget) performs poorly, and it appears to be when the MCMC is having trouble mixing. Overall, I think that we get an interesting perspective on how phylogenetic MCMCs “see” tree space with its peaks and valleys. Lots more to do!