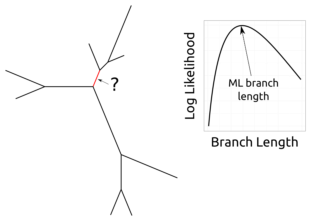
 Imagine we have a tree, sequence data for the leaves of that tree, and some fixed mutation rate matrix.
Then we fix all of the branch lengths of that tree except for one.
The likelihood function restricted to that branch gives a function from the positive real numbers to the unit interval.
Question: what is the shape of that function?
Imagine we have a tree, sequence data for the leaves of that tree, and some fixed mutation rate matrix.
Then we fix all of the branch lengths of that tree except for one.
The likelihood function restricted to that branch gives a function from the positive real numbers to the unit interval.
Question: what is the shape of that function?
I asked Vu this question when he arrived. As described in our new paper on arXiv, the answer is rather interesting, and more complex than I would have thought. Vu did a fantastic job with this project, taking (surprisingly to me) an algebraic approach, defining the characteristic polynomial of a likelihood function, defining an algebraic structure on conditional frequency patterns, then using a result about path-connected subgroups.
To summarize, if the model is quite simple (JC, F81), then the likelihood has a single maximum. However, more complex models such as K2P can take on arbitrarily weird shapes, such as having many global maxima. We’re not saying that this happens all the time or even that it happens much at all for real trees on real data, but we have developed foundations that allow us to analyze phylogenetic likelihoods in more detail. Having more such understanding will allow more confident statements about phylogenies and more effective tree reconstruction.