 Say we care about a function on pairs of trees (such as subtree-prune-regraft distance) that doesn’t make reference to the labels as such, but simply uses them as markers to ensure that the leaves end up in the right place.
We’d like to calculate this function for all trees of a certain type.
However, doing so for every pair of labeled trees is a waste, because if we just relabel the two trees in the same way, we will get the same result.
Say we care about a function on pairs of trees (such as subtree-prune-regraft distance) that doesn’t make reference to the labels as such, but simply uses them as markers to ensure that the leaves end up in the right place.
We’d like to calculate this function for all trees of a certain type.
However, doing so for every pair of labeled trees is a waste, because if we just relabel the two trees in the same way, we will get the same result.
So, how many computations do we actually need to do?
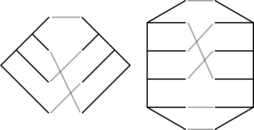
It turns out that we only need to do one calculation per tanglegram. A tanglegram is a pair of trees along with a bijection between the leaves of those trees. They have been investigated in coevolutionary analyses before, and there’s a considerable literature concerning how to draw them in the plane with the minimal number of crossings. However, the symmetries and number of tanglegrams on a given number of leaves have not been explored until now.
We recently posted two papers to the arXiv on tanglegrams. In the first, a mathematical phylogenetics paper, we do a preliminary algebraic and combinatorial study of tanglegrams, including unrooted and/or unordered tanglegrams (the picture above shows a rooted and an unrooted tanglegram). There we describe in detail how tanglegrams are equivalent to certain double cosets of the symmetric group. In the second, a combinatorics paper, we (mostly my coauthors Billey and Konvalinka) derive an explicit formula for the number of rooted ordered tanglegrams. This is pretty cool– there isn’t an equivalent formula for tree shapes (i.e. unlabeled trees not embedded in the plane). The derivation is lovely.
In any case, by using tanglegrams rather than pairs of trees, one gets an order-factorial (of the number of leaves) reduction in computation. Now we are applying this knowledge of tanglegrams with our high school student Kate to learn about tree space.