 In our previous work, Chris Whidden and I have been working to understand properties of phylogenetic Markov chain Monte Carlo (MCMC) by learning about the graph formed by all phylogenetic trees (as vertices) and tree rearrangements (as edges).
These tree rearrangements are ways of modifying one tree to get another.
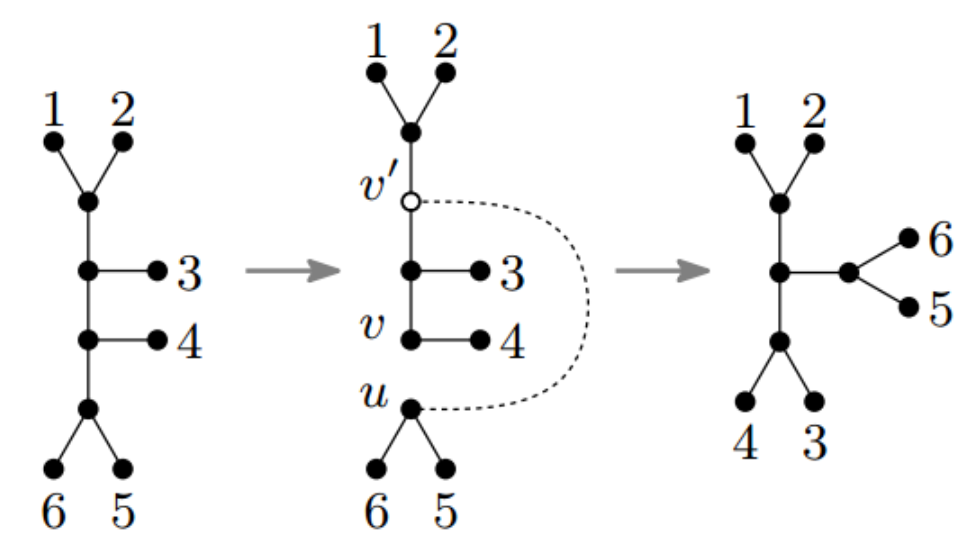
For example, here we have a picture of modifying a tree via so-called unrooted SPR.
In our previous work, Chris Whidden and I have been working to understand properties of phylogenetic Markov chain Monte Carlo (MCMC) by learning about the graph formed by all phylogenetic trees (as vertices) and tree rearrangements (as edges).
These tree rearrangements are ways of modifying one tree to get another.
For example, here we have a picture of modifying a tree via so-called unrooted SPR.
It’s natural to ask for the shortest path in this graph between two vertices, i.e. the number of unrooted SPR moves required to modify one tree to make another. The number of such moves is called the unrooted SPR (uSPR) distance. It turns out that the problem is hard in general but fixed parameter tractable, meaning that the complexity isn’t too bad for pairs of trees that aren’t too different from one another. The current best algorithm for unrooted SPR distance cannot compute distances larger than 7, or reliably compare trees with more than 30 leaves. This is in rather stark contrast to the rooted case, for which Chris’ latest algorithms can compute rooted SPR (rSPR) distances of greater than 50 with hundreds of taxa. The construct behind efficient algorithms for rSPR is called an agreement forest; a 2001 theorem due to Allen and Steel shows that computing rSPR distance is equivalent to finding a maximum agreement forest.
Thus, in order to try to improve the state of algorithms for the uSPR distance, our original goal was to define an agreement-forest like object for the unrooted case. This didn’t work! In fact Chris came up with some wild counter-examples showing that every characteristic one might want in an agreement forest does not hold in the unrooted case (see this tweet for a picture). These examples guided the rest of our work.
In the end, we developed a new distance, called the replug distance that bounds the uSPR distance below and is much more computable than full uSPR. Chris then developed a clever algorithm to use this and other approximate uSPR distances together to calculate the full uSPR distance. This algorithm can compute uSPR distances as large as 14 between trees with up to 50 leaves. He also proved a conjecture from 2008 that certain type of tree simplification preserves uSPR distance.
The paper describing these results just went up on arXiv. We tried to make it as simple and explicit as possible, but it ended up being a rather long and technical beast of a paper with a lot of custom notation and intermediate definitions. Nevertheless, it’s a real Whidden opus.
For my part, I was hoping to connect the uSPR distance with a more established area of mathematics so that we could leverage some powerful existing machinery. In particular, the theory of matroids seemed like a good fit, as the matroid independence condition could be used to ensure that all intermediate graph structures were actually trees. This didn’t seem to be helpful in the end, although it did get us started thinking about socket forests. I’d be glad to hear any ideas that anyone else has for connecting this sort of work with other parts of math.