Posterior probability estimation of phylogenetic tree topologies from an MCMC sample is currently a pretty simple affair. You run your sampler, you get out some tree topologies, you count them up, normalize to get a probability, and done. It doesn’t seem like there’s a lot of room for improvement, right?
Wrong.
Let’s step back a little and think like statisticians. The posterior probability of a tree topology is an unknown quantity. By running an MCMC sampler, we get a histogram, the normalized version of which will converge to the true posterior in the limit of a large number of samples. We can use that simple histogram estimate, but nothing is stopping us from taking other estimators of the per-topology posterior distribution that may have nicer properties.
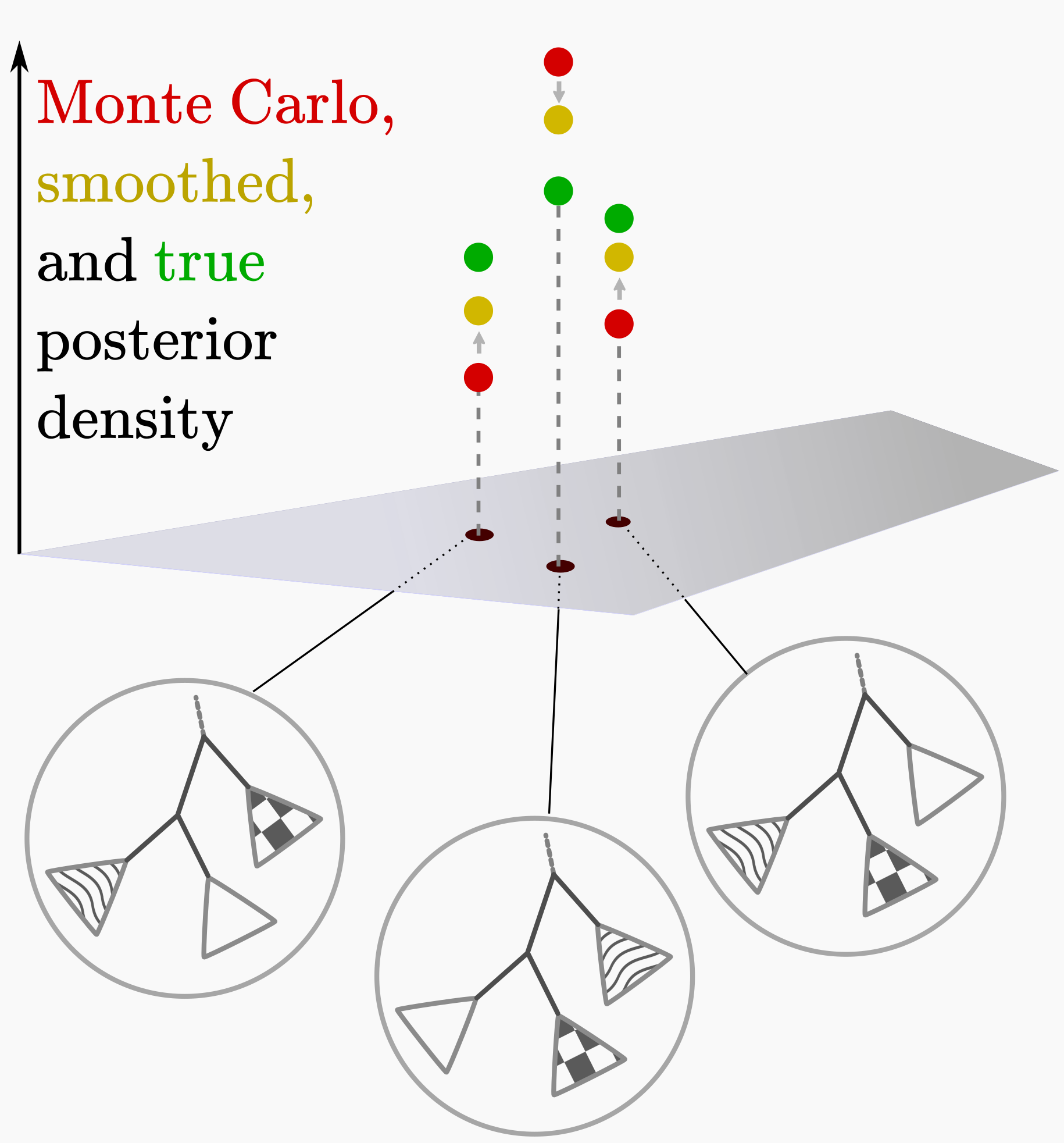
For real-valued samples we might use kernel density estimates to smooth noisy sampled distributions, which may reduce error when sampling is sparse. Because the number of phylogenies is huge, MCMC is computationally expensive, and we are naturally impatient, one is often in the sparsely-sampled regime for topology posteriors. Can we smooth out stochastic under- and over-estimates of topology posterior probabilities by using similarities between trees? (See upper-right cartoon.) This smoothing should also extend the posterior to unsampled topologies.
The question is, then, how do we do something like a kernel density estimate in tree space? In a beautiful line of work started by Höhna and Drummond and extended by Larget one can think of each tree as being determined by local choices about how groups of leaves (“clades”) get split apart recursively down the tree. Their work assumed independence between these clade splitting probabilities.
This is a super-cool idea, but the formulation didn’t seem to work well for tree probability estimation from posterior samples on real data. For example, Chris Whidden and I noticed that this procedure underestimated the posterior for sub-peaks and overestimated the posterior between peaks. This says that the conditional independence assumption on clades made by this method was too strong. But this doesn’t doom the entire approach! We just need to take a more flexible family of distributions over phylogenetic tree topologies.
I suggested this direction to Cheng Zhang, a postdoc in my group, and within a week he figured out the right construction that generalized this earlier work but allowed for much more complex distributions. Cheng’s construction parameterizes a tree in terms of “subsplits,” which are the choices about how to split up a given clade. To allow for more complex distributions than the previous conditional independence assumptions allow, he encodes tree probabilities in terms of a collection of subsplit-valued random variables that are placed in a Bayesian network.
The simplest such network enables dependence of a subsplit on the parent subsplit, which in tree terms means that when assigning a probability to a given subsplit we are influenced by what the sister clade is. More complex networks can encode more complex dependence structures. To our surprise, the simplest formulation worked well: allowing split frequencies for clades to depend on the sister clade gives a sufficiently flexible set of distributions to be able to fit complex tree-valued distributions.
In the simplest version one can write out the probability for a given tree like so:
where the qs are inferred probability distributions that we call conditional subsplit distributions.
In addition to more complex dependence structure, Cheng’s approach also more formally treats this whole procedure as an exercise in estimating an approximating distribution. Where previous efforts estimated probabilities by counting, one can do better in the unrooted case for subsplit networks by optimizing the parameterized distribution on trees to match an empirical sampled distribution of unrooted trees via expectation maximization. One can also take some weak priors to handle the sparsely-sampled case.
We’ve written up these results in a paper that has been accepted to the NeurIPS (previously NIPS1) conference as a Spotlight presentation. I’m proud of Cheng for this accomplishment, but consequently the paper is written more for a machine-learning audience rather than a phylogenetics audience. If you aren’t familiar with the Bayesian network formalism it may be a tough read. The key thing to keep in mind that the network (paper Figure 2) encodes the tree as a collection of subsplits assigned to the nodes of the network, and the edges describe probabilistic dependence. For example, the reason we can think of a conditional subsplit distribution as conditioning on the sister clade (see figure above) is because parent-child relationships in the subsplit Bayesian networks must take values such that the child subsplit is compatible with the parent subsplit.
If you don’t read anything else, flip to Table 1 and check out how much better these estimates are on big posteriors from real data than what everyone does right now, which is just to use the simple fraction. Magic! Hopefully it makes sense that we are smoothing out our MCMC posterior, and extending it to unsampled trees. If you have questions, I hope you will head on over to Phylobabble and ask them— let’s have a discussion!
Subsplit Bayesian networks open up a lot of opportunities for new ways of inferring posteriors on trees. Stay tuned!
We are always looking for folks to contribute in this area. If you’re interested, get in touch!
1: I’m happy to report that the NIPS conference has changed its name to NeurIPS. This is an important move that at signals at least a desire by the board for diversity and inclusion in machine learning. We can all hope that it is followed with concrete action.